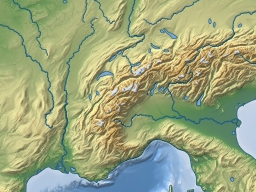
Importance rating problems

The importance rating for the rivers i described in the third part is based on the assumption that a rivers upstream continuation at a junction where two tributaries merge is always the one with the larger upstream length. As i demonstrated with the Saône/Rhone and Aar/Rhine examples this is not always correct.

In case of the Saône/Rhone the Rhone is larger river despite having the shorter cumulative upstream length since it originates from a high precipitation mountain area while the Saône originates from much drier areas.

In case of the Aar/Rhine the Aar is actually the larger river although it is common understanding that despite this the Rhine is the main river while the Aar is only a tributary.

In both cases non-uniform mapping, i.e. the fact that one of the tributaries watersheds is mapped in more detail than the other plays only a minor role. Similar examples exist in various parts of the world. The whole problem cannot be solved without taking additional information into account like the name of the rivers (if the name of one of the tributaries is identical to the downstream continuation it hints this is to be the more important one).

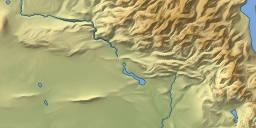
Interrupted rivers

Despite my attempt to fix errors on the Openstreetmap data like gaps in the path of a river there are cases where gaps prevail during the process. This can show up in the final map in two forms: Rivers ending without connection to other rivers or the ocean although in reality they are connected and rivers missing despite their size because the gaps prevent an accurate importance rating. Most of these cases have their origin at reservoirs where the river is not continued through the dam as in this case. There are currently additional problems with interrupted rivers like in case of the Tigris river further downstream which occur in rendering and are not actually part of the processing.

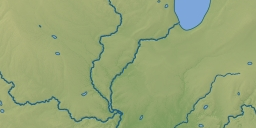
Faulty connections

There is also the opposite problem of river network connections where there should be none. This is usually the result of errors in the data as well although it can also occur if two waterbodies are very close despite being actually separate in the data. The clearest example is the connection between the Mississippi river system and Lake Michigan. This connection is formed by this canal which has no tag indicating it is artificial and is therefore processed like any other river.

In other cases it is often an insuspicious small connection very far upstream that can cause misinterpretation like here. There are heuristrics in place meant to prevent these connections to affect the importance ranking but this does not always work.

Lack of separation

A somewhat related problem is the lack of proper separation in the rendering at low zoom levels. As already mentioned in the fourth part this is not yet implemented. This leads to rivers connecting in their upper parts although no such connection exists in the data or is actually generated during processing.

Flat area flow structure problems

Apart from these specific problems there is a general issue with determining the river system structure in flat areas. Since the direction of waterways cannot be relied upon in the OSM data i determine it with help of elevation data. This is not precise enough in flat areas though and together with frequent bifurcations in those areas this leads to problems determining the waterflow. Again a good example is the Mississippi river where the Atchafalaya River is incorrectly assumed to be the main mouth of the river.