Isosurface object speedup patch - technical documentation

The POV-Ray 3.5 isosurface object is a very powerful tool for generating complex procedural geometry. A major problem limiting the use of this object is the bad performance when using slow functions, especially with high gradients. This patch is trying to improve this aspect.

The basic concept of the isosurface root finder in POV-Ray 3.5 is to sample the isosurface function along the ray. An upper limit for the gradient of the function (max_gradient) has to be given to achieve reasonable render times.

The interval of the ray within the isosurface container shape is recursively subdivided and the isosurface function is evaluated at the interval borders. This is continued until either the function values indicate that there can't be an intersection in this particular interval when the gradient of the function is less than max_gradient or the interval length has reached the required accuracy value. This method can be understood as a Lipschitz Method [3][4].

Several other methods for direct raytracing of implicit surfaces have been suggested but most of them either do not reliably find all intersections for arbitrary functions (Newton's method and regula falsi) or require additional information about the isosurface function (methods based on interval arithmetic or affine arithmetic) [14][15].

The most common method for rendering implicit surfaces, especially in non-raytracing systems, is polygonization. The surface is approximated with a polygon mesh. This technique usually much improve render speed since very efficient methods exist for raytracing meshes. The render speed is completely independent from the evaluation time of the isosurface function in this case.

The major disadvantages of this method are the significant time that is required to generate a high quality approximation of the surface and the amount of memory required for storing the mesh. Since one of the main advantages of procedural geometry is the low memory requirement this strongly limits the use of this approach. Most tesselation algorithms also have problems with high curvature surfaces.

patch description

This POV-Ray patch takes a different approach to improve the performance of isosurface renders. In plain POV-Ray 3.5 the whole segment of the ray that passes the container object has to be sampled for every ray-shape intersection test [1]. A rudimentary caching technique speeds up subsequent rays that don't intersect the isosurface but it only works for the camera rays. Since POV-Ray already contains a very efficient octree bounding system that is used for mesh and blob objects it was fairly straight away to use this for the isosurface object as well. This reduces the area that has to be tested for intersections and thereby avoids a lot of function evaluations at render time.

The bounding tree is generated by subdividing the container shape volume in an octree scheme and to select those cells that can possible contain the isosurface.

Of course the bounding tree increases memory consumption and parsing time but by changing the minimum grid size of the bounding tree the user has detailed control over this. I contrast to tesselation techniques a low detail precalculation grid also has no negative influence on the quality of the results.

The critical aspect of generating the bounding tree is the algorithm used for subdividing grid nodes. The goal is not to generate more nodes than those really containing the surface but at the same time avoid gaps that will result in holes in the render result.

There are two steps when generating the tree:

1. deciding if a node can contain parts of the surface and should be further subdivided.
2. to determine if a node is actually saved in the tree when the minimum grid size has been reached.

Three methods were implemented for these tasks:

method 1

This method is based on a given max_gradient value like the original isosurface algorithm. Starting from the whole container volume space is subdivided as long as the function values at all corners meet the following condition:

The subdivision is continued until the subdivision has reached a prescribed size limit. When the limit has been reached the nodes the formula above is still valid for are saved in the bounding tree.

To optimize performance a different max_gradient can be specified for the parse time subdivision process and for the render time root solving.

method 2

For the subdivision process this method works just like method 1.

When the subdivision limit has been reached the condition for storing the grid node in the bounding tree is

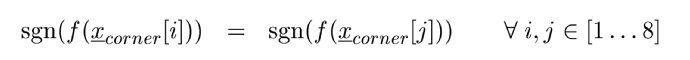
Note this condition is not met for all nodes containing parts of the surface with arbitrary functions. Therefore method 2 is less safe but it will generate much tighter bounds for arbitrary functions.

isosurface	method 1	method 2

method 3

Method 3 also uses the sign based condition for the subdivision process. This is even more critical since the validity of this condition is strongly related to the curvature of the surface in comparison to the tested node size.

grid size

The limit for the grid size can be adjusted in the isosurface object parameters. It can be a fixed value or a function that returns a value depending on the position. With such a function the detail level of the bounding tree can be adjusted to the requirements in different parts of the scene.

To avoid errors with method 2 and 3 it can be useful to sample other points than the node corners in addition. The patch implements an option to sample the midpoints of the node sides.

variable parameters

With the old isosurface root finder it would often be useful to adjust the parameters max_gradient and accuracy to different values in different parts of the scene. The advantages would in many cases be eaten up by the overhead of evaluating the function for these parameters. With the bounding tree it is no problem to store these values with the nodes.

In addition I implemented an adaptive max_gradient feature that uses the difference between the corner values of the node and an overestimation factor to specify the maximum gradient:

alternative root solver

In addition to the bounding techniques i implemented an alternative root solver. It is based on the sphere tracing technique described in [2] and [5].

Examples and performance comparison

I put together some samples showing the performance gain of the patch as well as possible problems.

literature

Here i put together a list of references to papers that i read while developing this patch as well as links to other related material.

[1] Ryoichi Suzuki describes some of the technique used in the POV-Ray 3.5 isosurface root solver in the following newsgroup posting:

Subject: Re: Isosurface and function pattern in v3.5
Date: Fri, 7 Sep 2001 12:41:09 +0900
Newsgroups: povray.general
From: "R. Suzuki" 
news://news.povray.org/3b984214@news.povray.org
http://news.povray.org/3b984214@news.povray.org

[2] Hyper-Rendering of Hyper-Textured Surfaces
Steve P. Worley and John C. Hart

[3] A Lipschitz Method for Accelerated Volume Rendering
Barton T. Stander and John C. Hart

[4] Ray Tracing Implicit Surfaces
John C. Hart

[5] Sphere tracing: a geometric method for the antialiased ray tracing of implicit surfaces
John C. Hart

More of John C. Hart's papers can be found on his website

[6] Implicit Surfaces
Jules Bloomenthal

[7] Polygonization of Implicit Surfaces
Jules Bloomenthal

More of Jules Bloomenthal's papers can be found on his website

[8] A Survey of Animation Related Implicit Surface Papers
Matthew Jondrow

[9] Adaptive Implicit Surface Polygonization using Marching Triangles
Samir Akkouche and Eric Galin

[10] An Overview of Implicit Surfaces
Agata Opalach and Steve Maddock

[11] Robust and Efficient Ray Intersection of Implicit Surfaces
Ole Caprani, Lars Hvidegaard, Mikkel Mortensen and Thomas Schneider

[12] Improving the Robustness and Accuracy of the Marching Cubes Algorithm for Isosurfacing
Adriano Lopes and Ken Brodlie
IEEE Transactions on visualization and Computer Graphics, Vol. 9, No. 1, January-March 2003

[13] On Marching Cubes
Gregory M. Nielson
IEEE Transactions on visualization and Computer Graphics, Vol. 9, No. 3, July-September 2003

[14] Sampling Procedural Shaders Using Affine Arithmetic
W. Heidrich, Ph. Slusallek, and H.-P. Seidel

[15] Surface intersection using affine arithmetic
Luiz Henrique de Figueiredo