Eine Eigenschaft der OpenStreetMap-Daten, welche Jedem bewußt sein sollte, der die Daten verwendet und welche Jeder, der mit den Daten in größerem Umfang arbeitet, früher oder später bemerkt, ist die uneinheitliche Qualität der Daten. Die Küstenlinien, mit denen ich in letzter Zeit recht viel gearbeitet habe sind in dieser Hinsicht ein Spezialfall, da sie die einzigen Daten in OpenStreetMap darstellen, welche routinemäßig im OpenStreetMap-Projekt in ihrer Gesamtheit verarbeitet werden. Aus diesem Grund gibt es bei diesen eine gewisse Garantie der Daten-Konsistenz – wenngleich diese fortlaufende Anstrengungen erfordert wie in Jochen Topf's Statusbericht beschrieben. Diese Konsistenz der Daten sagt jedoch noch nichts über ihre Genauigkeit aus, welche zu beurteilen ich hier versuchen möchte.

Ich habe zuvor bereits geschrieben, dass die OpenStreetMap Küstenlinien-Daten einen recht guten Qualitätsstandard erreicht haben, habe diese Behauptung jedoch nicht nachprüfbar belegt. Die große Schwierigkeit bei der Beurteilung der Genuaigkeit geographischer Daten liegt darin, dass man dafür eigentlich einen deutlich genaueren Referenzdatensatz benötigt. Konkret wäre für die Beurteilung der Genauigkeit einer Küstenlinie eine präzise Kenntnis der tatsächlichen Form der Küste notwendig.

Während es lokal in manchen Gegenden sicher detailliertere Daten gibt, als in Openstreetmap, sind in den meisten Fällen diese Daten nicht so viel genauer, dass man die Unterschiede zu den OSM-Daten vollständig als Ungenauigkeit der letzteren interpretieren könnte. Alle globalen Datensätze (einige sind im Openstreetmap wiki aufgezählt) sind zumindest in weiten Teilen weniger detailliert als die OpenStreetMap-Daten und eignen sich deshalb sowieso nicht als Referenz.

Beurteilung der Datenqualität ohne Referenz

Letztendlich müssen wir überlegen, wie man die Qualität ohne eine Referenz abschätzen kann. Naheliegend scheint, die Dichte der Datenpunkte in den Linien zu bestimmen. Die Küstenlinien sind in den Daten als Linienzüge vorhanden, Reihen von Punkten verbunden mit geraden Linien (was genau gerade in diesem Fall bedeutet werde ich wann anders mal dikutieren). Je dichter die Datenpunkte liegen, desto besser kann die tatsächliche Küstenlinie abgebildet werden. Aber es gibt zwei Probleme bei diesem Ansatz: Zum einen lässt sich ein sehr gerader Küstenlinienabschnitt recht genau mit nur sehr wenigen Punkten darstellen. Zum anderen kann eine Küstenlinie selbst mit sehr vielen Punkten ungenau sein, falls die Punkte garnicht an der tatsächlichen Küste liegen.

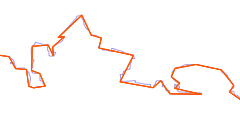
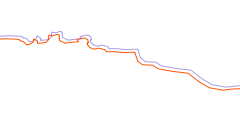
Krumme Küstenlinie mit ungenauer Erfassung	Gerade Küstenlinie mit genauer Erfassung	Küstenlinie mit detaillierter aber ungenauer Erfassung

Das zweite Problem ist ohne Referenzdaten nicht lösbar – im einfachsten Fall einer konstanten Verschiebung der Daten wie im obigen Beispiel sehen die Daten abgesehen von der Verschiebung genau so aus, wie die tatsächliche Küstenlinie und sind dennoch nicht korrekt. Das erste Problem lässt sich jedoch berücksichtigen. Die wichtigste Unterschied zwischen den roten Linien im ersten und zweiten Bild oben liegt in den Winkeln zwischen den Liniensegmenten an den Knoten. Deren Berechnung liefert neben der Knoten-Dichte einen zusätzlichen Wert zur Charakterisierung der Daten.

Bevor ich jetzt die Küstenlinien-Daten analysiere möchte ich einen Schritt zurücktreten und sehen, was wir hier eigentlich betrachten. Dies erfordert ein gewisses Verständnis davon, wie die betrachteten Daten erfasst werden. Im Fall von OpenStreetMap variiert dies etwas, die Daten basieren jedoch fast immer auf Luft- oder Satellitenbildern. Der Bearbeitungsprozess wird in den folgenden Bildern dargestellt:

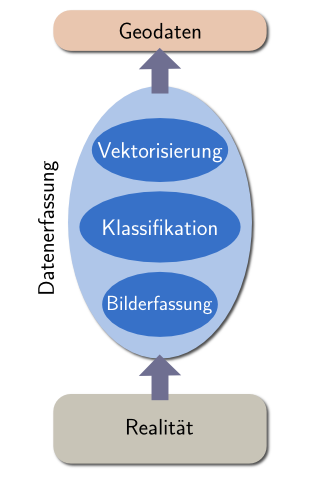
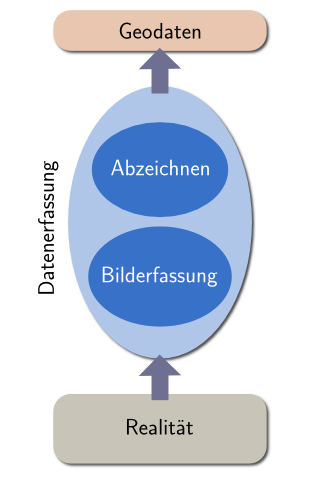
Küstenlinien-Erfassung basierend auf Bild-Klassifikation	Küstenlinien-Erfassung durch manuelles Abzeichnen von Bildern

Die meisten Küstenlinien Datensätze wie auch der Teil der Openstreetmap-Daten, welcher von anderswo importiert wurde (das sind insbesondere PGS-Daten) sind auf Basis von Satellitenbildern durch Wasser/Land-Klassifikation und anschließende Vektorisierung der Klassifikationsmaske produziert. Die durch die OSM-Gemeinschaft erfassten Daten sind im Wesentlichen durch Abzeichnen von Bildern per Hand produziert.

Da wie gesagt keine geeigneten Referenzdaten zur Verfügung stehen, sind die Möglichkeiten, diesen Prozess im Detail zu betrachten, beschränkt. Da wir nur das Endprodukt analysieren können, betrachten wir die Zwischenschritte nur durch den Filter der nachfolgenden Bearbeitungen. Hierdurch ergibt sich zwar ein sehr klarer Blick auf den Vektorisierungsschritt, bzw. das Abzeichnen, die Datenqualität wird jedoch vor allem auch von den davor liegenden Schritten beeinflusst und wir können diese nur indirekt und nur mit Hilfe von Annahmen über die Vektorisierung oder das Abzeichnen betrachten.

Analyse der Daten

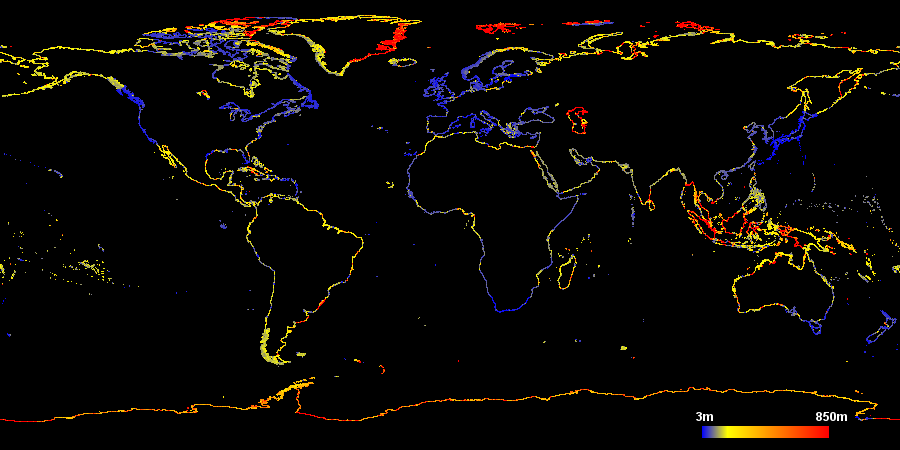
Ich beginne mit der Auswertung des durchschnittlichen Abstands zwischen den Küstenlinien-Punkten auf der Erdoberfläche. Die Farbe der Pixel im nachfolgenden Bild repräsentiert die durchschnittliche Länge der Küstenlinien-Segmente im Gebiet des jeweiligen Pixels.

Durch Klick auf das Bild können Sie eine größere Version anzeigen. Man sieht, dass der durchschnittliche Punktabstand starken Schwankungen unterliegt. Diese Schwankungen scheinen weder zufällig zu sein noch sind sie klar mit Unterschieden in der Form der tatsächlichen Küstenlinie verbunden. Die Obergrenze von 850m in der Darstellung hat keine besondere Bedeutung, es gibt einige kleinere Bereiche, in denen der durchschnittliche Abstand noch deutlich größer ist.

Klar erkennbar ist, dass die Bereiche der Erde, die auch ansonsten in Openstreetmap detailliert erfasst sind, insbesondere Europa und Japan, eine hohe Punktdichte in der Küstenlinie aufweisen – was auch nicht anders zu erwarten ist. Interessanter sind einige abrupte Änderungen in der Punktdichte, so zum Beispiel an der Grenze zwischen Alaska und Kanada zu sehen oder der Unterschied zwischen der Ost- und Westküste Grönlands.

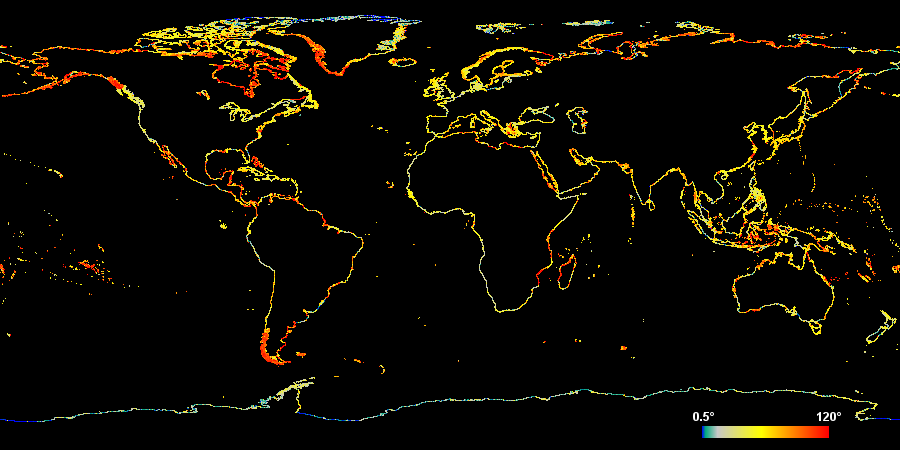
Als nächstes eine ähnliche Darstellung des durchschnittlichen Winkels zwischen den Liniensegmenten an den Knoten. Ein Winkel von Null Grad bedeutet, dass sich der Knoten direkt in der Mitte zwischen dem vorigen und dem nächsten Knoten befindet und 90 Grad entsprechen einem rechtwinkligen Knick in der Linie an diesem Punkt.

Zunächst einmal ist bemerkenswert, dass der durchschnittliche Winkel recht groß ist (das globale Mittel liegt bei 63 Grad). Auf der hier betrachteten Größenskala (zwischen einigen wenigen und einigen hundert Metern) gibt es in der Küstenlinie der Erde nur wenige klar definierte scharfe Ecken. Folglich deutet ein großer durchschnittlicher Winkel darauf hin, dass die Daten keine besonders gute Näherung für die in den als Grundlage verwendeten Bildern sichtbare Küstenlinie darstellen. In anderen Worten: durch eine detailliertere Vektorisierung oder präziseres manuelles Abzeichnen hätte man auf Basis der selben Datengrundlage deutlich genauere Daten produzieren können. Warum wurde dies nicht getan? Der Grund hierfür ist im Allgemeien Datensparsamkeit. Bei der Datenerfassung ist oft nicht die maximale Genauigkeit das Ziel und gleichzeitig bestehen oft enge Grenzen in Bezug auf das Datenvolumen.

Die meisten Gebiete mit durchgehend großen Winkeln (die roten bis orangenen Bereiche in der Karte oben) sind Gegenden, in denen PGS-Daten importiert wurden. Diese Daten weisen eine recht einheitliche Signatur sowohl in Bezug auf den durchschnittlichen Knotenabstand als auch bei den Winkeln auf. Dies kann man besonders gut im südlichen Alaska, in Südchile sowie in Westgrönland sehen. Diese Signatur hat ihre Ursache vermutlich in dem verwendeten Vektorisierungs-Verfahren. Das bedeutet jedoch nicht, dass alle mit automatischen Verfahren erzeugten Küstenlinien-Daten derart einheitliche Eigenschaften aufweisen. Ganz im Gegenteil wird eine effiziente Vektorisierungstechnik die Knotendichte an die Krümmung der Linie anpassen. Dies lässt sich zum Beispiel bei der Küste im Westen Polens beobachten (wobei diese vermutlich per Hand gezeichnet wurde). Der durchschnittliche Knotenabstand ist hier recht groß, mit am Größten in Europa, während der durchschnittliche Winkel sehr niedrig ist. Da die tatsächliche Küstenlinie hier ziemlich gerade ist, reichen wenige Knoten aus, um diese recht genau abzubilden.

Da es auf diesem Maßstab wie gesagt wenige wirkliche Ecken in der Küstenlinie gibt, kann man recht gut von einem optimalen Segmentwinkel an den Knoten von etwa 10-20 Grad ausgehen. Wie nahe die Daten an diesem Optimum liegen, sagt nichts über deren Genauigkeit aus, wohl aber darüber, wie gut die Daten die ihnen zu Grunde liegende Datenquelle abbilden. Ist der Winkel wesentlich größer wie im Falle der PGS-Daten, gingen Informationen, die in den Daten ursprünglich vorhanden waren, bei der Vektorisierung verloren. Ist der Winkel deutlich geringer, sind die Daten detaillierter als notwändig.

Unter Verwendung dieser Beobachtungen können wir nun versuchen, die beiden bisher einzeln betrachteten Werte zu einer gemeinsamen Qualitätskennzahl zusammenzufassen:

log(dist_avg*max(10, angle_avg))

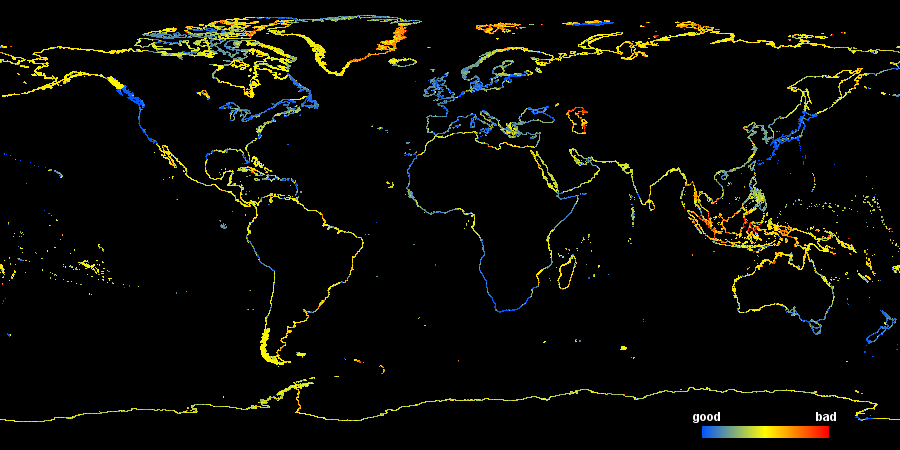
In Worte gefasst bedeutet diese Formel: Ein geringer Abstand zwischen den Knoten führt zu einem geringen Wert (entsprechend hoher Datenqualität), auch wenn der durchschnittliche Segmentwinkel groß ist. Ein geringer durchschnittlicher Segmentwinkel bewirkt auch bei großem Knotenabstand ebenso einen geringen kombinierten Wert, wobei Winkel von weniger als 10 Grad nicht verbessernd berücksichtigt werden. Der Logarithmus dient lediglich der passenden Skalierung. Der resultierende zusammengefasste Qualitätskennwert ist im folgenden Bild dargestellt:

Man sollte dieses Qualitätsmaß jedoch mit Vorsicht betrachten. Während die roten Bereiche höchstwahrscheinlich eine geringe Genauigkeit aufweisen, ist der Umkehtschluss, dass die blauen Bereiche von guter Qualität sind nicht ohne Weiteres möglich. Die Einschätzung schlägt insbesondere dann fehl, wenn die Daten deutlich geglättet wurden.

Die Karte zeigt vor allem drei Regionen, in denen die Datenqualität am dringensten verbessert werden müsste:

• Indonesien und Umgebung (insbesondere Malaysia, Thailand und Burma)
• Das Kaspische Meer
• Ostgrönland

Daneben gibt es einige kleinere Gebiete, die nicht besonders gut erfasst sind, insbesondere einige der polaren Inseln. Die drei genannten Regionen sind jedoch die größten Bereiche.

Auch erwähnt werden sollte, dass zumindest Indonesien in den PGS-Daten deutlich besser erfasst ist – anscheinend wurden diese in diesem Bereich nie importiert (oder nur in einer älteren und weniger detaillierten Version). Da jedoch inzwischen in dieser Region vieles per Hand erfasst wurde, würden großräumige Importe etwas schwierig.

Ein paar Einzelbeispiele und Zahlen

Zum Schluss möchte ich noch einige Einzelbeispiele sowie einige statistische Werte nennen:

Wie bereits erwähnt liegt der durchschnittliche Segmentwinkel für alle Daten bei 63 Grad. Der globale Mittelwert für den Knotenabstand beträgt 66 Meter, wodurch sich eine Gesamtlänge der Küstenlinie von 1.99 Millionen Kilometern ergibt. Das längste Segment (mit Ausnahme der Linienstücke, die die Küstenlinie bei 180 Grad schließen – diese wurden hier generell nicht berücksichtigt) ist 23.7 Kilometer lang. Hierbei handelt es sich jedoch nicht wirklich um einen Teil der Küstenlinie, sondern um einen Abschnitt vor der Mündung eines Flusses. Es gibt genau wie hier noch eine Reihe anderer Fälle, an denen die Küstenline weit vor der Mündung eines Flusses geschlossen wurde, was zu langen geraden Segmenten führt.

Die Bereiche, in denen die Daten am dringensten verbessert werden müssten, wurden bereits genannt. Ich möchte jetzt noch zwei Einzelbeispiele herausgreifen, wo die Genauigkeit besonders schlecht ist und zwar:

• Sulawesi (Indonesin)
• Ellesmere Island (Kanada)

Das erste Beipiel ist in der letzten Karte oben deutlich in tiefrot zu sehen, das Zweite jedoch nicht, obwohl hier Fjorde von mehr als 50km Länge vollständig fehlen. . Das liegt daran, dass hier die Daten anscheinend deutlich geglättet wurden. Die ursprüngliche Quelle für diese Daten lässt sich nicht ermitteln, sie könnten jedoch von älteren Karten auf Grundlage ungenauer oder unvollständiger Kartierungen der Gegend basieren.

Auf der positiven Seite der Regionen, wo die OSM-Küstenlinie besonders gut ist, möchte ich Estland herausgreifen, wo die Daten nicht nur sehr detailliert sind, sondern der durchschnittliche Segmentwinkel auch genau im beschriebenen optimalen Bereich liegt. Es gibt vermutlich auch einige Küstenlinien-Abschnitte im städtischen Bereich, wo die Erfassung sogar mit sub-Meter-Genauigkeit erfolgt ist, die werde ich im Rahmen dieser globalen Analyse jedoch nicht besonders betrachten.

Christoph Hormann, April 2013